Sample-based Krylov Quantum Diagonalization (SKQD)

This lesson on Sample-based quantum diagonalization (SKQD) combines methods explained in previous methods. It consists of a single example leveraging the Qiskit patterns framework:

• Step 1: Map problem to quantum circuits and operators
• Step 2: Optimize for target hardware
• Step 3: Execute using Qiskit Primitives
• Step 4: Post-process

An important step in the sample-based quantum diagonalization method is to generate quality vectors for the subspace. In the previous lesson, we used the LUCJ ansatz to generate subspace vectors for a chemistry Hamiltonian. In this lesson, we will use quantum Krylov states[1] as was discussed in lesson 2. First, we will review how to create the Krylov space on a quantum computer using time evolution operations. We will then sample from it. We will project the system Hamiltonian onto the sampled subspace and diagonalize it to estimate the ground state energy. The algorithm provably and efficiently converges to the ground state, under the assumptions described in lesson 2.

0. The Krylov space

Recall that a Krylov space $\mathcal{K}^r$ of order $r$ is the space spanned by vectors obtained by multiplying higher powers of a matrix $A$, up to $r-1$, with a reference vector $\vert v \rangle$.

If the matrix $A$ is the Hamiltonian $H$, the corresponding space is called the power Krylov space $\mathcal{K}_P$. In the case where $A$ is the time-evolution operator generated by the Hamiltonian $U=e^{-iH(dt)}$, the space is referred to as the unitary Krylov space $\mathcal{K}_U$. The power Krylov subspace cannot be generated directly on a quantum computer as $H$ is not a unitary operator. Instead, we can use the time-evolution operator $U = e^{-iH(dt)}$ which can be shown to give similar convergence guarantees as the power Krylov space. Powers of $U$ then become different time steps $U^k = e^{-iH(k dt)}$ where $k = 0, 1, 2, ..., (r-1)$.

1. Map problem to quantum circuits and operators

In this lesson, we consider the Hamiltonian for the antiferromagnetic XX-Z spin-1/2 chain with $L = 22$ sites with the periodic boundary condition:

from qiskit.transpiler import CouplingMap
from qiskit_addon_utils.problem_generators import generate_xyz_hamiltonian
 
num_spins = 22
coupling_map = CouplingMap.from_ring(num_spins)
H_op = generate_xyz_hamiltonian(coupling_map, coupling_constants=(0.3, 0.3, 1.0))

To construct the Krylov space, we need three main ingredients:

1. A choice of Krylov dimension ($r$) and time step ($dt$).
2. An initial (reference) state (vector $\vert v \rangle$ above) with polynomial overlap with target (ground) state, where the target state is sparse. This requirement for polynomial overlap is same as in the quantum phase estimation algorithm.
3. Time evolution operators $U^{k}=e^{-iH(k * dt)}$ ($k = 0, 1, 2, ..., r-1$).

For a chosen value of $r$ (and, $dt$), we will create $r$ separate quantum circuits and sample from them. Each quantum circuit is created by joining the quantum circuit representation of the reference state and the time evolution operator for a $k$ value.

A larger Krylov dimension improves the convergence of the estimated energy. We set the dimension to $5$ in this lesson to illustrate the convergence trend.

Ref [2] showed that a sufficiently small time step for KQD is $\pi / \vert \vert H \vert \vert$, and that it is preferable to underestimate this value rather than overestimate. On the other hand, choosing $dt$ to be too small leads to worse conditioning of the Krylov subspace, since the Krylov basis vectors differ less from timestep to timestep. In addition, while this choice of $dt$ is provably adequate for convergence of SKQD, in this sampling-based context the optimal choice of $dt$ in practice is a topic of ongoing study. In this lesson, we set $dt = 0.15$.

Besides Krylov dimension and time step, we need to set the number of Trotter steps for the time evolution. Using too few steps leads to larger Trotterization errors, while too many steps lead to deeper circuits. In this lesson, we set the number of Trotter steps to $6$.

# Set parameters for quantum Krylov algorithm
krylov_dim = 5  # size of krylov subspace
dt = 0.15
num_trotter_steps = 6

Next, we need to pick a reference state $\vert \psi \rangle$ that has some overlap with the ground state. For this Hamiltonian, we use the Neel state with alternating 1s and 0s $\vert ...101...010...101 \rangle$ as our reference state.

# Prep `Neel` state as the reference state for evolution
from qiskit import QuantumCircuit
 
qc_state_prep = QuantumCircuit(num_spins)
for i in range(num_spins):
    if i % 2 == 0:
        qc_state_prep.x(i)

Finally, we need to map the time evolution operator to a quantum circuit. This was done in lesson 2, but here we will leverage methods in Qiskit, specifically a method named synthesis. There are different methods to synthesize mathematical operators to quantum circuits with quantum gates. Many such techniques are available in Qiskit synthesis module. We will use the LieTrotter approach for synthesis [3] [4].

from qiskit.circuit import QuantumRegister
from qiskit.circuit.library import PauliEvolutionGate
from qiskit.synthesis import LieTrotter
 
evol_gate = PauliEvolutionGate(
    H_op, time=(dt / num_trotter_steps), synthesis=LieTrotter(reps=num_trotter_steps)
)  # `U` operator
 
qr = QuantumRegister(num_spins)
qc_evol = QuantumCircuit(qr)
qc_evol.append(evol_gate, qargs=qr)
 
circuits = []
for rep in range(krylov_dim):
    circ = qc_state_prep.copy()
 
    # Repeating the `U` operator to implement U^0, U^1, U^2, etc. for power Krylov space
    for _ in range(rep):
        circ.compose(other=qc_evol, inplace=True)
 
    circ.measure_all()
    circuits.append(circ)

circuits[1].decompose().draw("mpl", fold=-1)

Output:

circuits[2].decompose().draw("mpl", fold=-1)

Output:

2. Optimize for target hardware

Now that we have created the circuits, we can optimize them for a target hardware. We pick a utility scale QPU.

import warnings
 
from qiskit import generate_preset_pass_manager
from qiskit_ibm_runtime import QiskitRuntimeService
 
warnings.filterwarnings("ignore")
 
service = QiskitRuntimeService()
backend = service.backend("ibm_kyiv")

Now, we transpile the circuits to the target backend using a preset pass manager.

pm = generate_preset_pass_manager(backend=backend, optimization_level=3)
isa_circuits = pm.run(circuits=circuits)

3. Execute on target hardware

After optimizing the circuits for hardware execution, we are ready to run them on the target hardware and collect samples for ground state energy estimation.

from qiskit_ibm_runtime import SamplerV2 as Sampler
 
sampler = Sampler(mode=backend)
job = sampler.run(isa_circuits, shots=100_000)  # Takes approximately 2m 58s of QPU time

counts_all = [job.result()[k].data.meas.get_counts() for k in range(krylov_dim)]

4. Post-process results

Next, we aggregate the counts for increasing Krylov dimensions in a cumulative fashion. Using the cumulative counts, we will span subspaces for increasing Krylov dimension and analyze the convergence behavior.

from collections import Counter
 
counts_cumulative = []
for i in range(krylov_dim):
    counter = Counter()
    for d in counts_all[: i + 1]:
        counter.update(d)
 
    counts = dict(counter)
    counts_cumulative.append(counts)

To project and diagonalize the Hamiltonian, we use capabilities from qiskit-addon-sqd. The addon offers functionalities to project Pauli string-based Hamiltonians onto a subspace and solves for eigenvalues using SciPy.

from qiskit_addon_sqd.counts import counts_to_arrays
from qiskit_addon_sqd.qubit import solve_qubit

In principle, we can filter out bitstrings with incorrect pattern before spanning the subspace. For example, the ground state for the antiferromagnetic Hamiltonian in this lesson typically has an equal number of "up" and "down" spins, i.e., the number of "1"s in the bitstring should be exactly half the total number of bits (spins) in the system. The following function filters out bitstrings with incorrect number of "1"s from the counts.

# Filters out bitstrings that do not have specified number (`num_ones`) of `1` bits.
def postselect_counts(counts, num_ones):
    filtered_counts = {}
    for bitstring, freq in counts.items():
        if bitstring.count("1") == num_ones:
            filtered_counts[bitstring] = freq
 
    return filtered_counts

Using bitstrings with the correct number of up/down electrons, we span subspaces and compute eigenvalues for increasing Krylov dimension. Depending on the problem size and available classical resources, we may need to adopt subsampling (similar to the lesson on SQD) to keep the subspace dimension in check. Moreover, we can apply the notion of configuration recovery similar to Lesson 4. We can compute the electron occupancy per site from reconstructed eigenstates and use the information to correct bitstrings with an incorrect number of up/down electrons. We leave this as an exercise for interested readers.

import numpy as np
 
num_batches = 10
rand_seed = 0
scipy_kwargs = {"k": 2, "which": "SA"}
 
ground_state_energies = []
for idx, counts in enumerate(counts_cumulative):
    counts = postselect_counts(counts, num_ones=num_spins // 2)
    bitstring_matrix, probs = counts_to_arrays(counts=counts)
 
    eigenvals, eigenstates = solve_qubit(
        bitstring_matrix, H_op, verbose=False, **scipy_kwargs
    )
    gs_en = np.min(eigenvals)
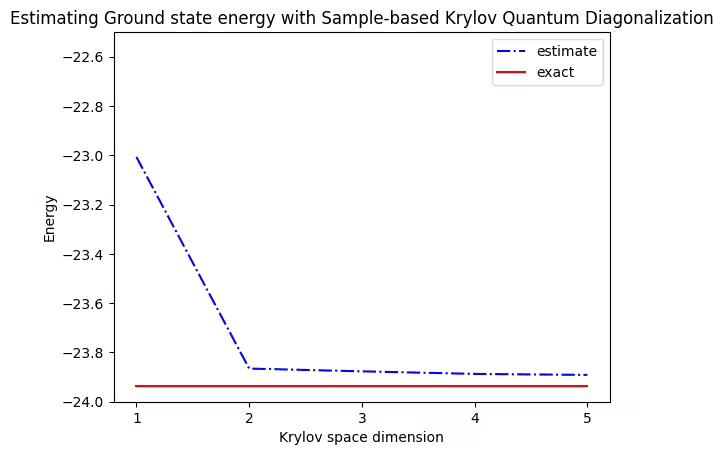
    ground_state_energies.append(gs_en)

Next, we plot computed energy as a function of Krylov dimension and compare with exact energy. The exact energy is computed separately using a classical Brute force method. We can see that the estimated ground state energy converges with increasing Krylov space dimension. Although Krylov dimension of $5$ is limiting, the results still show impressive convergence, which is expected to improve with a larger Krylov dimension [1].

import matplotlib.pyplot as plt
 
exact_gs_en = -23.934184
plt.plot(
    range(1, krylov_dim + 1),
    ground_state_energies,
    color="blue",
    linestyle="-.",
    label="estimate",
)
plt.plot(
    range(1, krylov_dim + 1),
    [exact_gs_en] * krylov_dim,
    color="red",
    linestyle="-",
    label="exact",
)
plt.xticks(range(1, krylov_dim + 1), range(1, krylov_dim + 1))
plt.legend()
plt.xlabel("Krylov space dimension")
plt.ylabel("Energy")
plt.ylim([-24, -22.50])
plt.title(
    "Estimating Ground state energy with Sample-based Krylov Quantum Diagonalization"
)
plt.show()

Output:

Check-in question

What could be done to improve the convergence in the plot above?

Answer:

Increase the Krylov dimension. In general, one could also increase the number of shots, but this is already quite high in the calculation above.

Check-in question

What are the principal advantages to SKQD over (a) SQD, and (b) KQD?

Answer:

There may be other valid answers, but complete answers should include the following:

(a) SKQD comes with convergence guarantees that SQD does not. In SQD you either need to make a very good guess for your ansatz that has excellent overlap with the ground state support in the computational basis, or you need to introduce a variational component to the calculation to sample a family of ansaetze.

(b) SKQD requires much less QPU time, because it avoids the costly calculation of matrix elements via the Hadamard test.

5. Summary

• Ground state energy estimations via sampling Krylov basis states is very well-suited to lattice models including spin systems, condensed matter problems, and lattice gauge theories. This approach scales much better than VQE, because it does not require optimization over many parameters in a variational ansatz as in VQE, or in heuristic ansatz-based SQD (e.g., the chemistry problem in the previous lesson).
  • To keep circuit depths low, it is wise to address lattice problems which are amenable to pre-fault tolerant hardware.
• SKQD does not incur a quantum measurement problem like in VQE. There are no groups of commuting Pauli operators to be estimated.
• SKQD is robust to noisy samples as one can use a problem-specific post-selection routine (for example, filter out bitstrings that do not adhere to problem-specific patterns) or incur classical diagonalization overhead (i.e., diagonalize in a larger subspace) to effectively remove the effect of noise.

References

[1] Jeffery Yu et al., "Quantum-Centric Algorithm for Sample-Based Krylov Diagonalization" (2025). arxiv:quant-ph/2501.09702.

[2] Ethan N. Epperly, Lin Lin, and Yuji Nakatsukasa. "A theory of quantum subspace diagonalization". SIAM Journal on Matrix Analysis and Applications 43, 1263–1290 (2022).

[2] N. Hatano and M. Suzuki, “Finding Exponential Product Formulas of Higher Orders” (2005). arXiv:math-ph/0506007.

[4] D. Berry, G. Ahokas, R. Cleve and B. Sanders, “Efficient quantum algorithms for simulating sparse Hamiltonians” (2006). arXiv:quant-ph/0508139.