Skip to main content
IBM Quantum Platform

Quantum algorithms: Phase estimation

Note

Kento Ueda (15 May 2024)

This notebook provides the fundamental concepts and implementation of the Quantum Fourier Transformation (QFT) and Quantum Phase Estimation (QPE).

PDFs of lecture notes will be available soon. Note that some code snippets may become deprecated since these are static images.

Approximate QPU time to run this experiment is 7 seconds.

1. Introduction

Quantum Fourier Transformation (QFT)

The Quantum Fourier Transformation is the quantum counterpart of the classical discrete Fourier transform. It is a linear transformation applied to the quantum states, mapping computational bases into their Fourier basis representations. The QFT plays a key role in many quantum algorithms, offering an efficient method to extract periodicity information from quantum states. The QFT can be implemented with O(N2)O(N^2) operations with quantum gates such as Hadamard gates and Control-Phase gates for NN qubits, enabling exponential speedup over classical Fourier transformation.

  • Applications: It is a foundational part in quantum algorithms such as Shor's algorithm for factoring large integers and discrete logarithm.

Quantum Phase Estimation (QPE)

Quantum Phase Estimation is a quantum algorithm used to estimate the phase associated with an eigenvector of a unitary operator. This algorithm provides a bridge between the abstract mathematical properties of quantum states and their computational applications.

  • Applications: It can solve problems such as finding eigenvalues of unitary matrices and simulating quantum systems.

Together, QFT and QPE form the essential backbone of many quantum algorithms solving problems that are infeasible for classical computers. By the end of this notebook, you will gain an understanding of how these techniques are implemented.

2. Basic of Quantum Fourier Transformation (QFT)

from qiskit import QuantumCircuit, QuantumRegister, ClassicalRegister
from qiskit_aer import AerSimulator
from qiskit.visualization import plot_histogram, plot_bloch_multivector
from qiskit.quantum_info import Statevector
from qiskit.transpiler.preset_passmanagers import generate_preset_pass_manager
from qiskit_ibm_runtime import Sampler
 
from numpy import pi

From the analogy with the discrete Fourier transform, the QFT acts on a quantum state ∣X⟩=∑j=0N−1xj∣j⟩\vert X\rangle = \sum_{j=0}^{N-1} x_j \vert j \rangle for NN qubits and maps it to the quantum state ∣Y⟩=∑k=0N−1yk∣k⟩\vert Y\rangle = \sum_{k=0}^{N-1} y_k \vert k \rangle.

QFTN:∣j⟩↦1N∑k=0N−1ωNjk∣k⟩QFT_{N}: \vert j \rangle \mapsto \frac{1}{\sqrt{N}}\sum_{k=0}^{N-1}\omega_N^{jk} \vert k \rangle

where ωNjk=e2πijkN\omega_N^{jk} = e^{2\pi i \frac{jk}{N}}.

Or the unitary matrix representation:

UQFT=1N∑j=0N−1∑k=0N−1ωNjk∣k⟩⟨j∣U_{QFT} = \frac{1}{\sqrt{N}} \sum_{j=0}^{N-1} \sum_{k=0}^{N-1} \omega_N^{jk} \vert k \rangle \langle j \vert

2.1. Intuition

The quantum Fourier transform (QFT) transforms between two bases, the computational (Z) basis, and the Fourier basis. But what does the Fourier basis mean in this context? You likely recall that the Fourier transform F(ω)F(\omega) of a function f(x)f(x) describes the convolution of f(x)f(x) onto a sinusoidal function with frequency ω\omega. In Layman's terms: the Fourier transform is a function describing how much of each frequency ω\omega we would need to build up a function f(x)f(x) out of sine functions (or cosine functions). To get a better sense for what the QFT means in this context, consider the stepped images below which show a number encoded in binary, using four qubits:

IFRAME

In the computational basis, we store numbers in binary using the states ∣0⟩|0\rangle and ∣1⟩|1\rangle.

Note the frequency with which the different qubits change; the leftmost qubit flips with every increment in the number, the next with every 2 increments, the third with every 4 increments, and so on.

If we apply a quantum Fourier transform to these states, we map

∣State in Computational Basis⟩→QFT∣State in Fourier Basis⟩|\text{State in Computational Basis}\rangle \quad \xrightarrow[]{\text{QFT}} \quad |\text{State in Fourier Basis}\rangle QFT∣x⟩=∣x~⟩\text{QFT}|x\rangle = |\widetilde{x}\rangle

(We often denote states in the Fourier basis using the tilde (~)).

In the Fourier basis, we store numbers using different rotations around the Z-axis:

IFRAME

The number we want to store dictates the angle at which each qubit is rotated around the Z-axis. In the state ∣0~⟩|\widetilde{0}\rangle, all qubits are in the state ∣+⟩|{+}\rangle. As seen in the example above, to encode the state ∣5~⟩|\widetilde{5}\rangle on 4 qubits, we rotated the leftmost qubit by 52n=516\tfrac{5}{2^n} = \tfrac{5}{16} full turns (516×2π\tfrac{5}{16}\times 2\pi radians). The next qubit is turned double this (1016×2π\tfrac{10}{16}\times 2\pi radians, or 10/1610/16 full turns), this angle is then doubled for the qubit after, and so on.

Again, note the frequency with which each qubit changes. The leftmost qubit (qubit 0) in this case has the lowest frequency, and the rightmost the highest.

2.2 Example: 1-qubit QFT

Let's consider the case of N=21=2N = 2^1 = 2.

The unitary matrix can be written:

UQFT=12∑j=01∑k=01ω2jk∣k⟩⟨j∣=12(ω20∣0⟩⟨0∣+ω20∣0⟩⟨1∣+ω20∣1⟩⟨0∣+ω21∣1⟩⟨1∣)=12(∣0⟩⟨0∣+∣0⟩⟨1∣+∣1⟩⟨0∣−∣1⟩⟨1∣)=H\begin{aligned} U_{QFT} & = \frac{1}{\sqrt{2}} \sum_{j=0}^{1} \sum_{k=0}^{1} \omega_2^{jk} \vert k \rangle \langle j \vert \\ & = \frac{1}{\sqrt{2}} (\omega_2^{0} \vert 0 \rangle \langle 0 \vert + \omega_2^{0} \vert 0 \rangle \langle 1 \vert + \omega_2^{0} \vert 1 \rangle \langle 0 \vert + \omega_2^{1} \vert 1 \rangle \langle 1 \vert) \\ & = \frac{1}{\sqrt{2}} (\vert 0 \rangle \langle 0 \vert + \vert 0 \rangle \langle 1 \vert + \vert 1 \rangle \langle 0 \vert - \vert 1 \rangle \langle 1 \vert) \\ & = H \end{aligned}

This operation is the result of applying the Hadamard gate (HH).

2.3 Product representation of QFT

Let's generalize a transformation for N=2nN = 2^n, QFTNQFT_{N} acting on the state ∣x⟩=∣x1…xn⟩\vert x \rangle = \vert x_1\ldots x_n \rangle.

QFTN∣x⟩=1N∑y=0N−1ωNxy∣y⟩=1N∑y=0N−1e2πixy/2n∣y⟩ since ωNxy=e2πixyN and N=2n=1N∑y=0N−1e2πi(∑k=1nyk/2k)x∣y1…yn⟩ rewriting in fractional binary notation y=y1…yn,y/2n=∑k=1nyk/2k=1N∑y=0N−1∏k=1ne2πixyk/2k∣y1…yn⟩ after expanding the exponential of a sum to a product of exponentials,=1N⨂k=1n(∣0⟩+e2πix/2k∣1⟩) after rearranging the sum and products, and expanding∑y=0N−1=∑y1=01∑y2=01…∑yn=01=1N(∣0⟩+e2πi2x∣1⟩)⊗(∣0⟩+e2πi22x∣1⟩)⊗…⊗(∣0⟩+e2πi2n−1x∣1⟩)⊗(∣0⟩+e2πi2nx∣1⟩)\begin{aligned} QFT_N\vert x \rangle & = \frac{1}{\sqrt{N}} \sum_{y=0}^{N-1}\omega_N^{xy} \vert y \rangle \\ & = \frac{1}{\sqrt{N}} \sum_{y=0}^{N-1} e^{2 \pi i xy / 2^n} \vert y \rangle ~\text{since}\: \omega_N^{xy} = e^{2\pi i \frac{xy}{N}} \:\text{and}\: N = 2^n \\ & = \frac{1}{\sqrt{N}} \sum_{y=0}^{N-1} e^{2 \pi i \left(\sum_{k=1}^n y_k/2^k\right) x} \vert y_1 \ldots y_n \rangle \:\text{rewriting in fractional binary notation}\: y = y_1\ldots y_n, y/2^n = \sum_{k=1}^n y_k/2^k \\ & = \frac{1}{\sqrt{N}} \sum_{y=0}^{N-1} \prod_{k=1}^n e^{2 \pi i x y_k/2^k } \vert y_1 \ldots y_n \rangle \:\text{after expanding the exponential of a sum to a product of exponentials,} \\ & = \frac{1}{\sqrt{N}} \bigotimes_{k=1}^n \left(\vert0\rangle + e^{2 \pi i x /2^k } \vert1\rangle \right) \:\text{after rearranging the sum and products, and expanding} \sum_{y=0}^{N-1} = \sum_{y_1=0}^{1}\sum_{y_2=0}^{1}\ldots\sum_{y_n=0}^{1} \\ & = \frac{1}{\sqrt{N}} \left(\vert0\rangle + e^{\frac{2\pi i}{2}x} \vert1\rangle\right) \otimes \left(\vert0\rangle + e^{\frac{2\pi i}{2^2}x} \vert1\rangle\right) \otimes \ldots \otimes \left(\vert0\rangle + e^{\frac{2\pi i}{2^{n-1}}x} \vert1\rangle\right) \otimes \left(\vert0\rangle + e^{\frac{2\pi i}{2^n}x} \vert1\rangle\right) \end{aligned}

2.4 Example: Circuit construction of 3 qubits QFT

From the above description, it may not be clear how to construct a QFT circuit. For now, simply note that we expect three qubits to have phases that evolve at different "rates". Understand exactly how this is translated into a circuit is left as an exercise to the reader. There are multiple diagrams and examples in the lecture pdf. Additional resources include this lesson from the Fundamentals of quantum algorithms course.

We will demonstrate QFT using simulators only, and thus we will not use the Qiskit patterns framework until we move on to quantum phase estimation.

# Prepare for 3 qubits circuit
qr = QuantumRegister(3)
cr = ClassicalRegister(3)
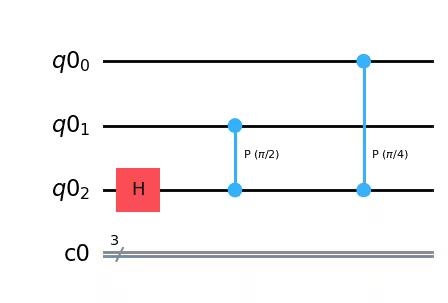
qc = QuantumCircuit(qr, cr)
qc.h(2)
qc.cp(pi / 2, 1, 2)  # Controlled-phase gate from qubit 1 to qubit 2
qc.cp(pi / 4, 0, 2)  # Controlled-phase gate from qubit 0 to qubit 2
qc.draw(output="mpl")

Output:

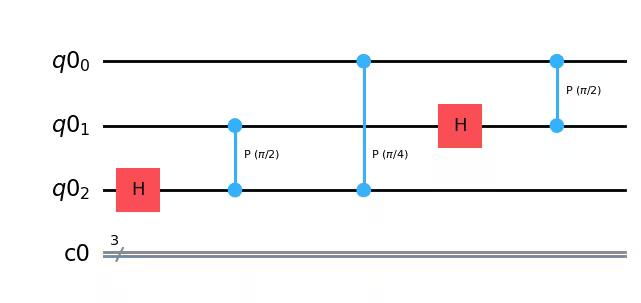
Output of the previous code cell 
qc.h(1)
qc.cp(pi / 2, 0, 1)  # Controlled-phase gate from qubit 0 to qubit 1
 
qc.draw(output="mpl")

Output:

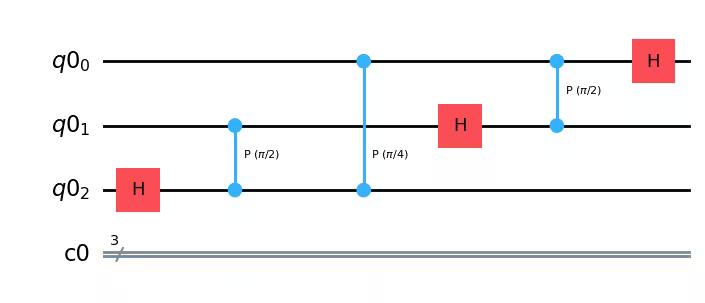
Output of the previous code cell 
qc.h(0)
 
qc.draw(output="mpl")

Output:

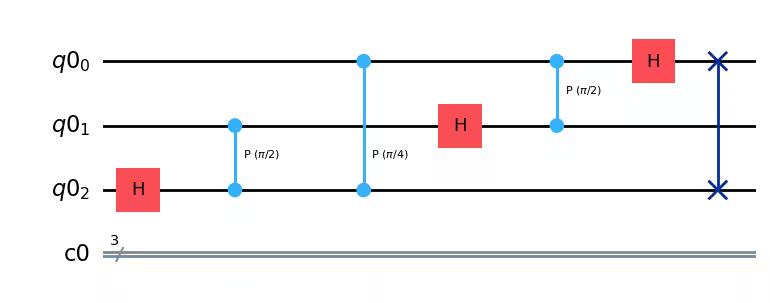
Output of the previous code cell 
qc.swap(0, 2)
 
qc.draw(output="mpl")

Output:

Output of the previous code cell

We try to apply QFT to ∣5⟩|5\rangle as an example.

First, we confirm the binary notation of the integer 5 and create the circuit encoding the state 5:

bin(5)

Output:

'0b101'

qc = QuantumCircuit(3)
 
qc.x(0)
qc.x(2)
qc.draw(output="mpl")

Output:

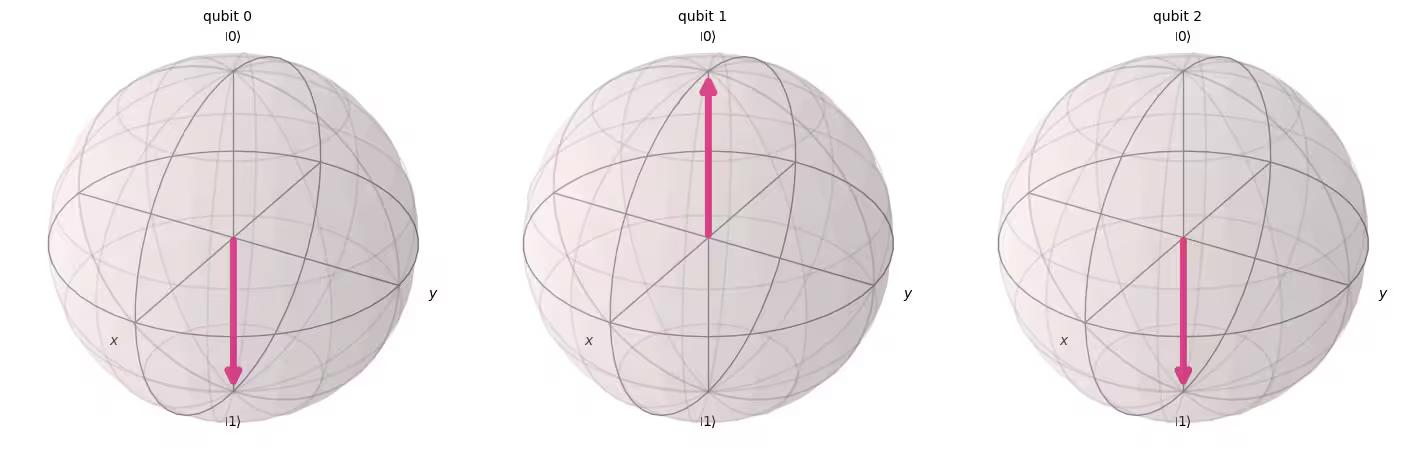
Output of the previous code cell

We check the quantum states using the Aer simulator:

statevector = Statevector(qc)
plot_bloch_multivector(statevector)

Output:

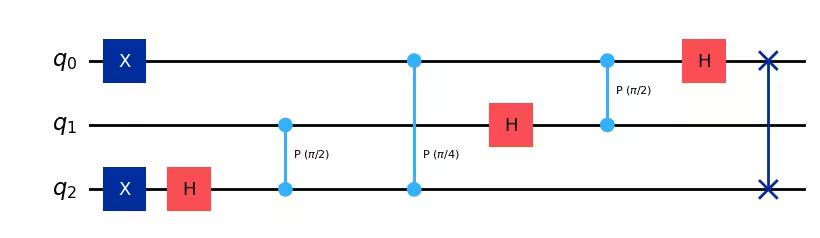
Output of the previous code cell

Finally, we add QFT and view the final state of our qubits:

qc.h(2)
qc.cp(pi / 2, 1, 2)
qc.cp(pi / 4, 0, 2)
 
qc.h(1)
qc.cp(pi / 2, 0, 1)
 
qc.h(0)
 
qc.swap(0, 2)
 
qc.draw(output="mpl")

Output:

Output of the previous code cell 
statevector = Statevector(qc)
plot_bloch_multivector(statevector)

Output:

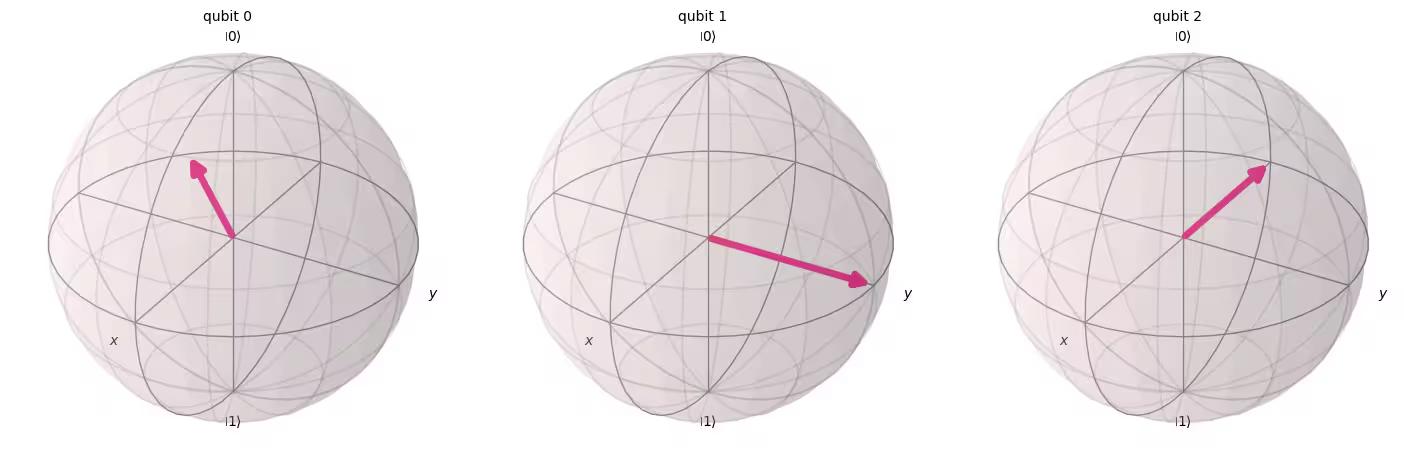
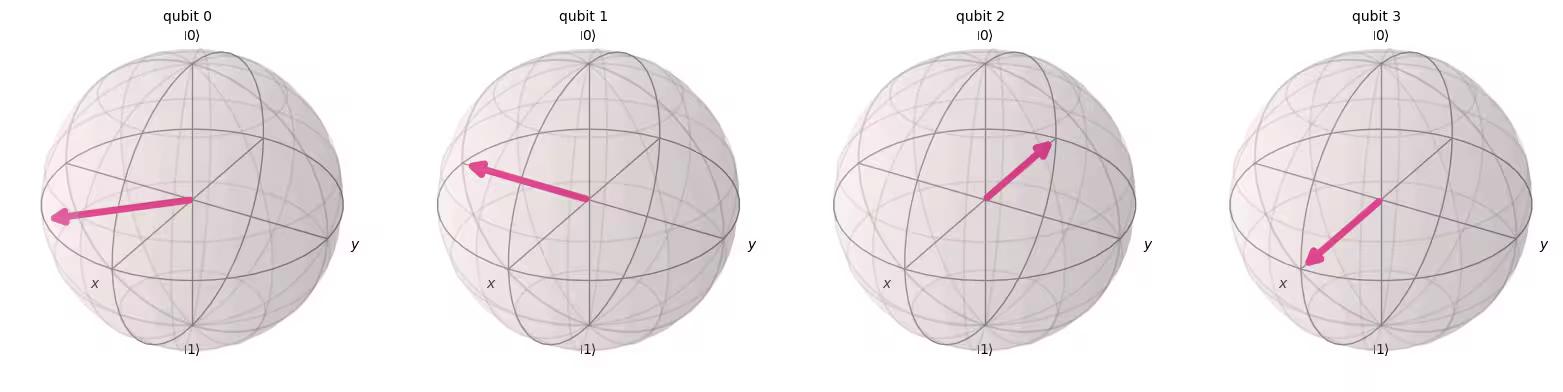
Output of the previous code cell

We can see out QFT function has worked correctly. Qubit 0 has been rotated by 58\tfrac{5}{8} of a full turn, qubit 1 by 108\tfrac{10}{8} full turns (equivalent to 14\tfrac{1}{4} of a full turn), and qubit 2 by 208\tfrac{20}{8} full turns (equivalent to 12\tfrac{1}{2} of a full turn).

2.5 Exercise: QFT

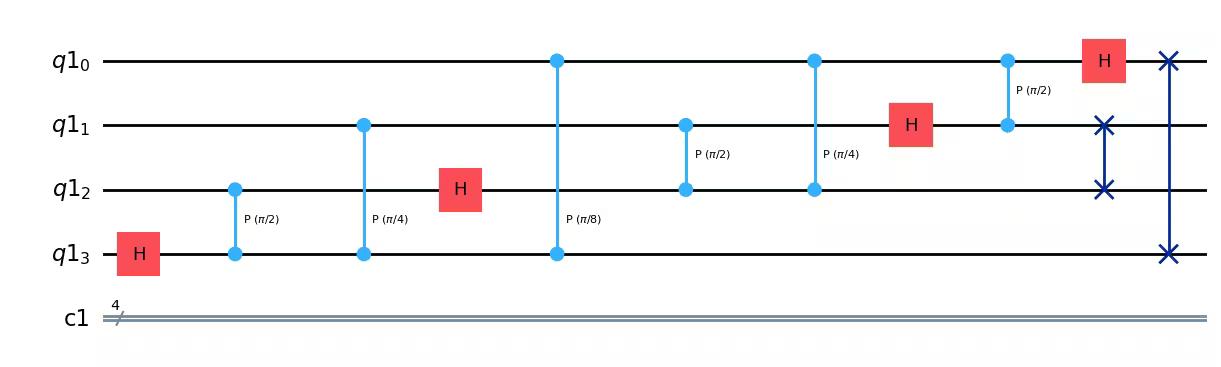
(1) Implement QFT of 4 qubits.

##your code goes here##

(2) Apply QFT to ∣14⟩|14\rangle, simulate and plot the statevector using the Bloch sphere.

##your code goes here##

Solution of the exercise: QFT

(1)

qr = QuantumRegister(4)
cr = ClassicalRegister(4)
qc = QuantumCircuit(qr, cr)
 
qc.h(3)
qc.cp(pi / 2, 2, 3)
qc.cp(pi / 4, 1, 3)
qc.cp(pi / 8, 0, 3)
 
qc.h(2)
qc.cp(pi / 2, 1, 2)
qc.cp(pi / 4, 0, 2)
 
qc.h(1)
qc.cp(pi / 2, 0, 1)
 
qc.h(0)
 
qc.swap(0, 3)
qc.swap(1, 2)
 
qc.draw(output="mpl")

Output:

Output of the previous code cell

(2)

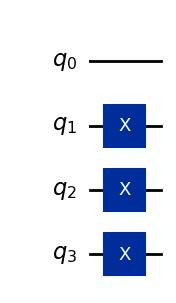
bin(14)

Output:

'0b1110'

qc = QuantumCircuit(4)
 
qc.x(1)
qc.x(2)
qc.x(3)
qc.draw("mpl")

Output:

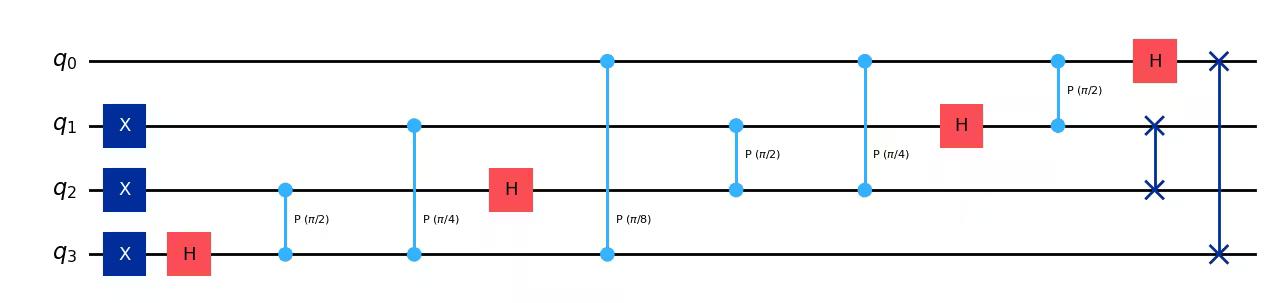
Output of the previous code cell 
qc.h(3)
qc.cp(pi / 2, 2, 3)
qc.cp(pi / 4, 1, 3)
qc.cp(pi / 8, 0, 3)
 
qc.h(2)
qc.cp(pi / 2, 1, 2)
qc.cp(pi / 4, 0, 2)
 
qc.h(1)
qc.cp(pi / 2, 0, 1)
qc.h(0)
 
qc.swap(0, 3)
qc.swap(1, 2)
 
qc.draw(output="mpl")

Output:

Output of the previous code cell 
statevector = Statevector(qc)
plot_bloch_multivector(statevector)

Output:

Output of the previous code cell

3. Basics of Quantum Phase Estimation (QPE)

Given a unitary operation UU, the QPE estimates θ\theta in U∣ψ⟩=e2πiθ∣ψ⟩U\vert\psi \rangle =e^{\boldsymbol{2\pi i} \theta }|\psi \rangle since UU is unitary, all of its eigenvalues have a norm of 1.

3.1 Procedure

1. Setup

∣ψ⟩\vert\psi\rangle is in one set of qubit registers. An additional set of nn qubits form the counting register on which we will store the value 2nθ2^n\theta:

∣ψ0⟩=∣0⟩⊗n∣ψ⟩|\psi_0\rangle = \lvert 0 \rangle^{\otimes n} \lvert \psi \rangle

2. Superposition

Apply a nn-bit Hadamard gate operation H⊗nH^{\otimes n} on the counting register:

∣ψ1⟩=12n2(∣0⟩+∣1⟩)⊗n∣ψ⟩|\psi_1\rangle = {\frac {1}{2^{\frac {n}{2}}}}\left(|0\rangle +|1\rangle \right)^{\otimes n} \lvert \psi \rangle

3. Controlled Unitary operations

We need to introduce the controlled unitary CUCU that applies the unitary operator UU on the target register only if its corresponding control bit is ∣1⟩|1\rangle. Since UU is a unitary operator with eigenvector ∣ψ⟩|\psi\rangle such that U∣ψ⟩=e2πiθ∣ψ⟩U|\psi \rangle =e^{\boldsymbol{2\pi i} \theta }|\psi \rangle, this means:

U2j∣ψ⟩=U2j−1U∣ψ⟩=U2j−1e2πiθ∣ψ⟩=⋯=e2πi2jθ∣ψ⟩U^{2^{j}}|\psi \rangle =U^{2^{j}-1}U|\psi \rangle =U^{2^{j}-1}e^{2\pi i\theta }|\psi \rangle =\cdots =e^{2\pi i2^{j}\theta }|\psi \rangle

3.2 Example: T-gate QPE

Let's use TT gate as an example of QPE and estimate its phase θ\theta.

T∣1⟩=(100eiπ4)(01)=eiπ4∣1⟩T|1\rangle = \begin{pmatrix} 1 & 0\\ 0 & e^\frac{i\pi}{4}\\ \end{pmatrix} \begin{pmatrix} 0\\ 1\\ \end{pmatrix} = e^\frac{i\pi}{4}|1\rangle

We expect to find:

θ=18\theta = \frac{1}{8}

where

T∣1⟩=e2iπθ∣1⟩T|1\rangle = e^{2i\pi\theta}|1\rangle

We initialize ∣ψ⟩=∣1⟩\vert\psi\rangle = \vert1\rangle of the eigenvector of TT gate by applying an XX gate:

qpe = QuantumCircuit(4, 3)
qpe.x(3)
qpe.draw(output="mpl")

Output:

Output of the previous code cell

Next, we apply Hadamard gates to the counting qubits:

for qubit in range(3):
    qpe.h(qubit)
qpe.draw(output="mpl")

Output:

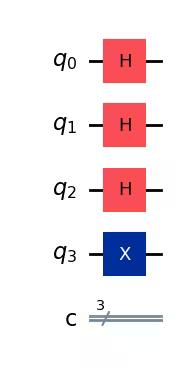
Output of the previous code cell

We perform the controlled unitary operations:

repetitions = 1
for counting_qubit in range(3):
    for i in range(repetitions):
        qpe.cp(pi / 4, counting_qubit, 3)  # This is C-U
    repetitions *= 2
qpe.draw(output="mpl")

Output:

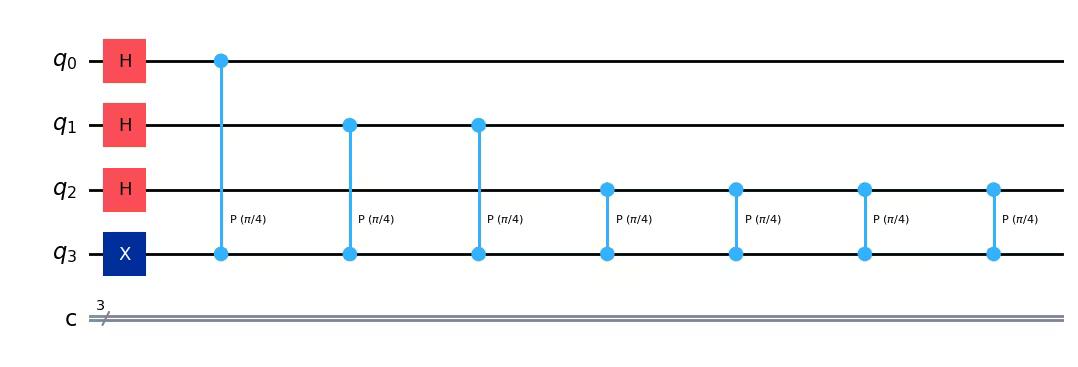
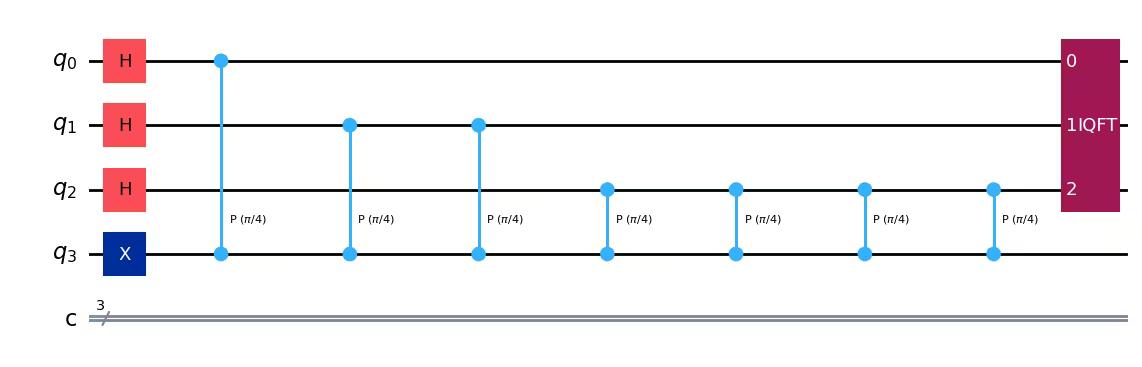
Output of the previous code cell

We apply the inverse quantum Fourier transformation to convert the state of the counting register, then measure the counting register:

from qiskit.circuit.library import QFT
# Apply inverse QFT
qpe.append(QFT(3, inverse=True), [0, 1, 2])
qpe.draw(output="mpl")

Output:

Output of the previous code cell 
for n in range(3):
    qpe.measure(n, n)
qpe.draw(output="mpl")

Output:

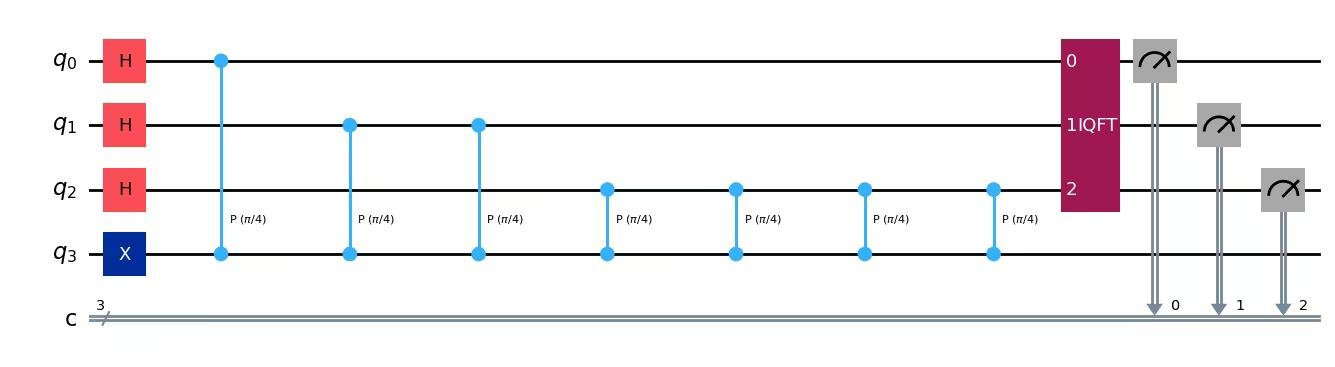
Output of the previous code cell

We can simulate using Aer simulator:

aer_sim = AerSimulator()
shots = 2048
 
pm = generate_preset_pass_manager(backend=aer_sim, optimization_level=1)
t_qpe = pm.run(qpe)
 
sampler = Sampler(mode=aer_sim)
job = sampler.run([t_qpe], shots=shots)
result = job.result()
answer = result[0].data.c.get_counts()
 
plot_histogram(answer)

Output:

Output of the previous code cell

We see we get one result (001) with certainty, which translates to the decimal: 1. We now need to divide our result (1) by 2n2^n to get θ\theta:

θ=123=18\theta = \frac{1}{2^3} = \frac{1}{8}

Shor's algorithm allows us to factorize a number by building a circuit with θ\theta unknown and obtaining θ\theta.

3.3 Exercise

Estimate θ=1/3\theta = 1/3 using 3 qubits for counting and a qubit for an eigenvector.

P∣1⟩=eiλ∣1⟩P|1\rangle = e^{i\lambda}|1\rangle. Since we want to implement U∣1⟩=e2πi13∣1⟩U|1\rangle = e^{2\pi i \tfrac{1}{3}}|1\rangle, we need to set λ=2π3\lambda = \tfrac{2 \pi}{3}.

##your code goes here##

Solution of the exercise: θ=1/3\theta = 1/3

# Create and set up circuit
qpe = QuantumCircuit(4, 3)
 
# Apply H-Gates to counting qubits:
for qubit in range(3):
    qpe.h(qubit)
 
# Prepare our eigenstate |psi>:
qpe.x(3)
 
# Do the controlled-U operations:
angle = 2 * pi / 3
repetitions = 1
for counting_qubit in range(3):
    for i in range(repetitions):
        qpe.cp(angle, counting_qubit, 3)
    repetitions *= 2
 
# Do the inverse QFT:
qpe.append(QFT(3, inverse=True), [0, 1, 2])
 
for n in range(3):
    qpe.measure(n, n)
 
qpe.draw(output="mpl")

Output:

Output of the previous code cell 
aer_sim = AerSimulator()
shots = 4096
 
pm = generate_preset_pass_manager(backend=aer_sim, optimization_level=1)
t_qpe = pm.run(qpe)
 
sampler = Sampler(mode=aer_sim)
job = sampler.run([t_qpe], shots=shots)
result = job.result()
answer = result[0].data.c.get_counts()
 
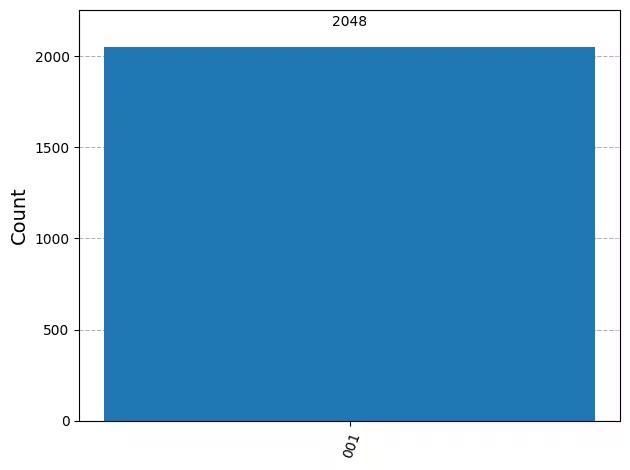
plot_histogram(answer)

Output:

Output of the previous code cell

4. Execution using the Qiskit Runtime Sampler primitive

We will perform QPE using the real quantum device and follow 4 steps of Qiskit patterns.

  1. Map the problem to a quantum-native format
  2. Optimize the circuits
  3. Execute the target circuit
  4. Post-process the results
from qiskit_ibm_runtime import QiskitRuntimeService
from qiskit_ibm_runtime import Sampler
# Loading your IBM Quantum account(s)
 
service = QiskitRuntimeService()

4.1 Step 1: Map problem to quantum circuits and operators

qpe = QuantumCircuit(4, 3)
qpe.x(3)
for qubit in range(3):
    qpe.h(qubit)
repetitions = 1
for counting_qubit in range(3):
    for i in range(repetitions):
        qpe.cp(pi / 4, counting_qubit, 3)  # This is C-U
    repetitions *= 2
qpe.append(QFT(3, inverse=True), [0, 1, 2])
for n in range(3):
    qpe.measure(n, n)
qpe.draw(output="mpl")

Output:

Output of the previous code cell 
backend = service.least_busy(simulator=False, operational=True, min_num_qubits=4)
 
print(backend)

Output:

<IBMBackend('ibm_strasbourg')>

4.2 Step 2: Optimize for target hardware

# Transpile the circuit into basis gates executable on the hardware
pm = generate_preset_pass_manager(backend=backend, optimization_level=2)
qc_compiled = pm.run(qpe)
 
qc_compiled.draw("mpl", idle_wires=False)

Output:

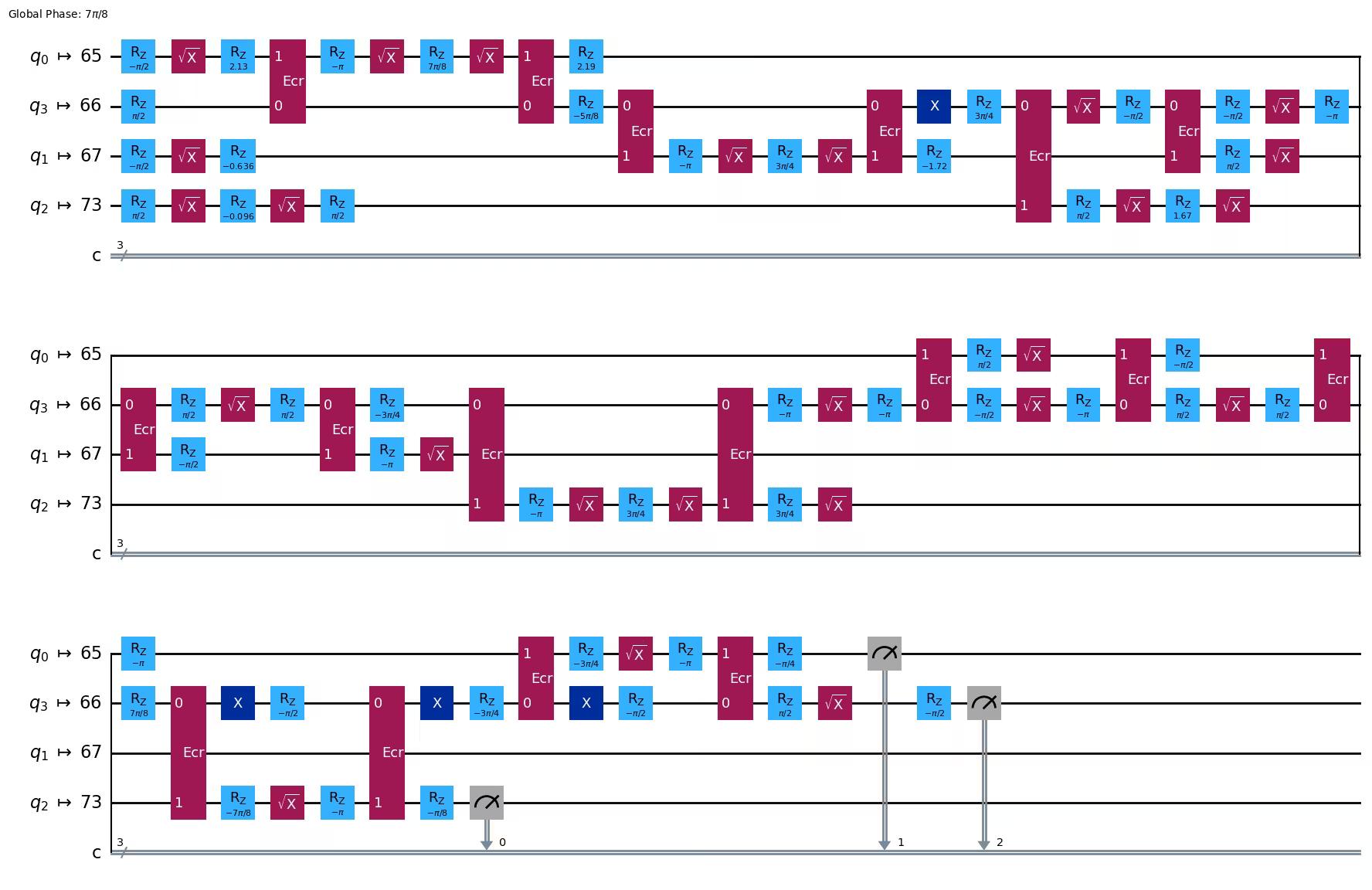
Output of the previous code cell

4.3 Step 3: Execute on target hardware

real_sampler = Sampler(mode=backend)
job = real_sampler.run([qc_compiled], shots=1024)
job_id = job.job_id()
print("job id:", job_id)

Output:

job id: d13p4zb5z6q00087ag00

job = service.job(job_id)  # Input your job-id between the quotations
job.status()

Output:

'DONE'

result_real = job.result()
print(result_real)

Output:

PrimitiveResult([SamplerPubResult(data=DataBin(c=BitArray(<shape=(), num_shots=1024, num_bits=3>)), metadata={'circuit_metadata': {}})], metadata={'execution': {'execution_spans': ExecutionSpans([DoubleSliceSpan(<start='2025-06-09 22:39:00', stop='2025-06-09 22:39:00', size=1024>)])}, 'version': 2})

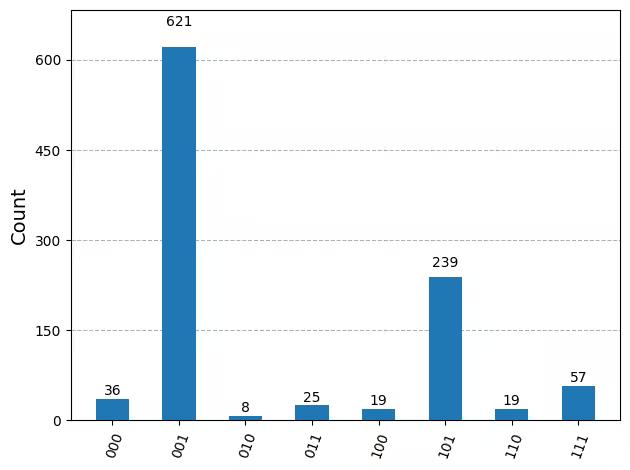
4.4 Step 4: Post-process the results

from qiskit.visualization import plot_histogram
 
plot_histogram(result_real[0].data.c.get_counts())

Output:

Output of the previous code cell 
# See the version of Qiskit
import qiskit
 
qiskit.__version__

Output:

'2.0.2'
Was this page helpful?
Report a bug or request content on GitHub.